Die Materie hat mehrere Eigenschaften. Ein Objekt kann z.B. eine Masse haben. Das ist eine Eigenschaft, die nur mit dem Objekt zu tun hat, egal wo das Objekt sich befindet oder in welcher Situation es ist. Die Masse ist ein charakteristisches Merkmal des Objektes so wie die Laung.
Ein Objekt kann positiv oder negativ geladen sein. Die Objekte, die wir im Leben normalerweise sehen bestehen alle aus 3 verschiedenen Elementarteilchen: Das Proton, das Elektron und das Neutron. Die Protonen sind positiv geladen, die Elektronen sind negativ geladen und die Neutronen sind elektrisch neutral, also nicht geladen.
Protonen und Elektronen haben umgekehrte Ladungen, und dabei meine ich, dass ihre Beträge gleich sind aber mit umgekehrten Vorzeichen. Dadurch kann man schon erkennen, dass Objekte mit gleicher Elektronen- und Protonenanzahl nicht geladen sind. Also positivgeladene Objekte haben mehr Protonen als Elektronen und negativ geladene Objekte genau das Gegenteil davon.
(Es gibt auch andere Elementarteilchen, außer Elektronen und Protonen, die geladen sind, z.B. Myonen sind negativ geladen. Diese komischen Partikel finden wir im Alltag normalerweise nicht.)
Da Elektronen und Protonen die Ladungen im Alltag verursachen, würde es schon Sinn machen, 1 Elektronenladung als Einheit für Ladung zu definieren. Diese Einheit gibt es ([e]\(\rightarrow\) Elementarladung), aber im Alltag sieht man sie kaum. Das liegt daran, dass die Ladungen im Alltag viel größer als [e] sind, deswegen ist die SI-Einheit das Coulomb [C].
Jetzt wird die Geschichte interessanter. Zwischen zwei Ladungen gibt es immer eine Kraft und diese Kraft wird durch die Coulomb-Gesetze beschrieben. Was wichtig zu merken ist:
-Gleiche Ladungen stoßen sich ab, ungleiche ziehen sich an. -Die Richtung von dieser Kraft verläuft als Verbindungsgerade zwischen den zwei Ladungen -Die Kraft auf die eine Ladung ist im Betrag gleich groß wie die auf die andere Ladung. Die Kräfte wirken aber in entgegengesetzter Richtung.

Mit \(\vec{F}_{21}=\frac{1}{4\pi\epsilon_0}\frac{Q_1Q_2}{d^2}\).
Diese Formel ist experimentell ermittelt worden, so dass wir zwei interessante Aspekte zu diskutieren haben, nähmlich welche Intuition wir aus der Formel ziehen können und wie sie experimentell ermittelt wurde.
Im Hinblick auf die Interpretation und die Intuition stellen wir fest, dass die Kraft eine Abhängigkeit der Form \(\frac{1}{d^2}\) und eine lineare Abhängigkeit von beiden Ladungen hat.
Dies entspricht unserer Intuition, dass je größer die Ladungen sind, desto größer ist die Kraft, und je größer der Abstand zwischen den Ladungen ist, desto geringer ist die Kraft. Die genaue Form, d.h. ob die Formel die Ladung, die Ladung zum Quadrat oder die auf 8 erhöhte Ladung sein wird, sowie ob der Abstand quadratisch oder in einer anderen Potenz erhöht wird, müssen wir an dieser Stelle experimentell ermitteln.
Der vorherige Faktor kann als eine Proportionalitätskonstante zwischen physikalischen Größen betrachtet werden. Ein kleiner historischer Exkurs ist angebracht, um zu sehen, wie diese Konstante definiert wurde.
Obwohl Charles-Augustin de Coulomb das Coulombsche Gesetz in seiner heutigen Form formulierte, war er nicht der erste, der die Kräfte zwischen elektrischen Ladungen beobachtete. Tatsächlich wurde seine Arbeit, die schließlich in dem Gesetz gipfelte, durch seine Studien über das von Joseph Priestley formulierte Gesetz der elektrischen Abstoßung motiviert. Um nicht nur die Abstoßung der Ladungen, sondern auch das mathematische Gesetz, das diese Abstoßung hat, zu überprüfen, entwickelte Coulomb einen Apparat mit einer Torsionswaage zur Messung der von den Ladungen ausgeübten Kraft. Für eine detailliertere Beschreibung der Apparatur empfehle ich den Artikel (https://www.aps.org/publications/apsnews/201606/physicshistory.cfm) oder den Text, der Coulombs ursprüngliches Experiment nachbildet: “Regular Twists: Replicating Coulomb’s Wire-Torsion Experiments – Peter Heering – Physics in perspective, 2006 (DOI:10.1007/s00016-005-0262-2)”.
Der Grundgedanke des Experiments ist, vereinfacht ausgedrückt, die Vorstellung, dass bestimmte Größen die elektrische Kraft zwischen zwei Objekten beeinflussen müssen. In diesem Fall wären diese Größen: die elektrischen Ladungen der Objekte und der Abstand zwischen ihnen.
Die beiden Faktoren müssen, zumindest anfangs, getrennt analysiert werden.
Betrachten wir zunächst den Einfluss von Ladungen auf die elektrische Kraft. Dazu müssen wir alle Größen gleich lassen, mit Ausnahme einer Ladung, die wir ändern müssen. Der Aufbau des Experiments selbst ist für die Diskussion im Moment nicht wichtig, aber es wäre so etwas wie das Coulomb-Experiment.
Die Betrachtung von Messfehlern werden wir mathematisch nicht berücksichtigen; wir sollten uns also bewusst sein, dass es sie gibt, ohne sie jedoch in Diagrammen und Messungen zu berücksichtigen.
Nehmen wir an, dass die folgenden Daten erzeugt wurden (Die konstante Ladung beträgt 1C und den Abstand zwischen Ladungen 1cm):
| Ladung (C) | Kraft (N) |
|---|---|
| \(1.00000000\cdot 10^{-8}\) | \(9340.272655319712\) |
| \(1.07142857\cdot 10^{-8}\) | \(10186.918300873147\) |
| \(1.14285714\cdot 10^{-8}\) | \(10929.478245117043\) |
| \(1.21428571\cdot 10^{-8}\) | \(10689.661780277745\) |
| \(1.28571429\cdot 10^{-8}\) | \(11701.686595860268\) |
| \(1.35714286\cdot 10^{-8}\) | \(11933.502246318825\) |
| \(1.42857143\cdot 10^{-8}\) | \(12826.467615956495\) |
| \(1.50000000\cdot 10^{-8}\) | \(12989.424488334736\) |
| \(1.57142857\cdot 10^{-8}\) | \(15099.564150672459\) |
| \(1.64285714\cdot 10^{-8}\) | \(14594.355896159565\) |
| \(1.71428571\cdot 10^{-8}\) | \(15438.382962028183\) |
| \(1.78571429\cdot 10^{-8}\) | \(16838.56922073084\) |
| \(1.85714286\cdot 10^{-8}\) | \(16052.043961239753\) |
| \(1.92857143\cdot 10^{-8}\) | \(17876.487941995732\) |
| \(2.00000000\cdot 10^{-8}\) | \(18006.225461291873\) |
Bei einer solchen Tabelle ist es schwierig, Trends in den Daten zu erkennen, deswegen verwenden Wissenschaftler gerne grafische Darstellungen.
Die Daten in der Tabelle können wie folgt dargestellt werden:

Ein naiver Ansatz wäre, sich vorzustellen, dass alle Punkte korrekt gemessen wurden, komplett ohne Messfehler und dass die Funktion, die die elektrische Kraft beschreibt, in etwa so aussieht:

Dieser Ansatz würde scheitern, wenn ein weiteres Experiment mit leicht abweichenden Werten durchgeführt wird.
Tatsache ist, dass wir Messfehler haben, die immer vorkommen. Eine viel vernünftigere Aussage wäre also, dass die Funktion eine Gerade ist und, dass die Punkte von der Geraden abweichen wegen experimenteller Messfehler.
Wie die Zuverlässigkeit des Ansatzes zu bewerten ist, soll hier nicht behandelt werden, ist aber ein sehr interessanter Bereich der Mathematik.
Unsere Aufgabe besteht nun darin, die beste gerade Linie zu finden, die den experimentellen Daten beschreibt.
Wie auch immer,haben wir hier einen Durchbruch erzielt. Wahrscheinlich hat die Formel für die elektrische Kraft die folgende Form:
\(\vec{F}_{el}=konstante\cdot g(d)\cdot Q_1\cdot Q_2\)
Im Grunde genommen sagen wir, dass die Kraft eine lineare Funktion der Ladung die wir ändern ist, aber auch, dass sie gleichzeitig eine lineare Funktion der Ladung die wir nicht ändern ist. Das liegt daran, dass es keinen Unterschied macht, ob man die eine oder die andere Ladung im Experiment ändert.
Wir sagen auch, dass die anderen Einflüsse auf die elektrische Kraft sind: Eine Funktion, die von der Entfernung abhängt (wir kennen die Form noch nicht) und möglicherweise eine Konstante, die die Steigung der Geraden bestimmt.
Durch die Bestimmung der linearen Funktion, die die Daten am besten beschreibt, haben wir eine der Informationen, die wir zur Bestimmung der Formelkonstante benötigen.
Dies motiviert die folgende Frage: Was bestimmt eine gute lineare Funktion zur Beschreibung der Punkte? Eine gute Möglichkeit wäre: Die Linie, die den kleinsten Abstand zwischen den Punkten hat, ist die beste Linie, um die Punkte zu beschreiben.
Der Abstand, den wir hier berechnen werden, mag zunächst etwas seltsam erscheinen, aber wir werden seine Bedeutung klären.
Lass uns ein Beispiel mit 3 Punkten betrachten und dann versuchen wir, eine Linie zu finden, die sie am besten beschreibt:
Betrachten wir die folgenden Punkte \((1,1); (3,4); (5,5)\).
Der Gedanke hinter einer Funktion, die die Punkte beschreibt, ist, dass man durch die Eingabe eines Wertes von \(x\) in der Funktion einen genauen Wert von \(y\) vorhersagen kann. Der Abstand, der uns interessiert, ist also nicht der normale Abstand zwischen Punkt und Gerade, sondern die Differenz zwischen den \(y\) Werten von Punkt und Gerade. Das bedeutet, dass es bei den Punkten \((x_1,y_1); (x_2,y_2); (x_3,y_3)\) und einer linearen Funktion \(f(x)=y\) der Abstand zwischen Punkt 1 und der Geraden wie folgt berechnet wird:
\(Entfernung1=f(x_1)-y_1\)
Und die Gesamtentfernung ist die Summe der einzelnen Entfernungen:
\(Entfernung=Entfernung1+Entfernung2+Entfernung3\)
\(=f(x_1)-y_1+f(x_2)-y_2+f(x_3)-y_3\)
Oder, grafisch ausgedrückt:


Nach der obigen Definition sehen wir, dass im ersten Diagramm die Unterschiede (grün dargestellt) zwischen den Punkten und die Gerade 1, -1 bzw. 4 betragen. Im zweiten Diagramm sind die Abstände 1, -4 und 1. Es passiert, dass manche Abstände positiv und manche negativ sind, weil einige Abstände nach oben und andere nach unten verlaufen. Aus diesem Grund kann es vorkommen, dass sich positive und negative Abstände gegenseitig abkürzen und die Nähe einer Geraden zu den Punkten falsch dargestellt werden. Damit diese Art von Problem nicht auftritt, betrachten wir nicht nur die Entfernung, sondern die Entfernung zum Quadrat. Negative Zahlen zum Quadrat werden ebenfalls positiv, so dass sich jeder Abstand addiert, ohne dass es zu Abkürzungen kommt.
Die neue Formel lautet dann
\(Entfernung=Entfernung1+Entfernung2+Entfernung3\)
\(=(f(x_1)-y_1)^2+(f(x_2)-y_2)^2+(f(x_3)-y_3)^2\)
Unser Ziel ist es nun, eine Gerade zu finden, die diesen Wert so klein wie möglich macht, so dass wir hoffentlich die beste Gerade haben, um die Punkte zu beschreiben.
Zurück zum Beispiel der Coulomb-Kraft: Wir Finden die Formel für die Gerade mit dem kleinsten Abstand.
\(F(Q)=a\cdot Q\)
Um genauer zu sein, müssen wir einen Wert für \(a\) finden, i.e. die Steigung der Gerade. Die Gesamtenfernung \(d\) der Gerade \(F(Q_i)\) und eine gemessene Kraft \(F_i\) berechnen wir als:
\(d=(F(Q_1)-F_1)^2+\cdots+(F(Q_{15})-F_{15})^2\)
\(d=(a\cdot 1.00000000\cdot 10^{-8}-9340.272655319712)^2+\cdots+(a\cdot 2.00000000\cdot 10^{-8}-18006.225461291873)^2\)
Für alle 15 Messungen. Das alles zusammengefasst ergibt:
\(d=3.517857142857143\cdot10^{-15}\cdot a^2 – 0.006386251872470817\cdot a + 2.901651961807952×10^9\)
Das mag hässlich aussehen, aber es ist nur eine nach oben geöffnete quadratische Funktion mit \(a\) als Variabel, dessen Tiefpunkt wir relativ einfach finden können, nähmlich: \(a=\frac{2922202802030456692518}{3219381949}\).
Das bedeutet, dass die Konstante und die Abstandsfunktion zusammen diesen Wert ergeben. Da wir noch nicht wissen, wie die Funktion von der Entfernung abhängt, können wir noch nicht sagen, welchen Wert die Konstante hat.
Um die Form der Funktion zu finden, die von dem Abstand abhängt, brauchen wir ein ähnliches Experiment, bei dem wir jedoch den Abstand und nicht mehr die Ladungen variieren. Um die Rechnungen einfacher zu machen nehmen wir an, dass die beiden Ladungen 1 Coulomb betragen.
| Abstand (m) | Kraft (N) |
|---|---|
| \(1000\) | \(9038.00667310924\) |
| \(1071.42857143\) | \(7786.126938715384\) |
| \(1142.85714286\) | \(6879.672836576199\) |
| \(1214.28571429\) | \(6093.655976256048\) |
| \(1285.71428571\) | \(5569.697306286453\) |
| \(1357.14285714\) | \(4829.864478837498\) |
| \(1428.57142857\) | \(4452.906294240747\) |
| \(1500\) | \(4154.926224819538\) |
| \(1571.42857143\) | \(3656.088087477773\) |
| \(1642.85714286\) | \(3308.6104841873193\) |
| \(1714.28571429\) | \(2906.460493770968\) |
| \(1785.71428571\) | \(2791.370742205006\) |
| \(1857.14285714\) | \(2643.7939347650877\) |
| \(1928.57142857\) | \(2557.6869591173386\) |
| \(2000\) | \(2254.7325257088346\) |
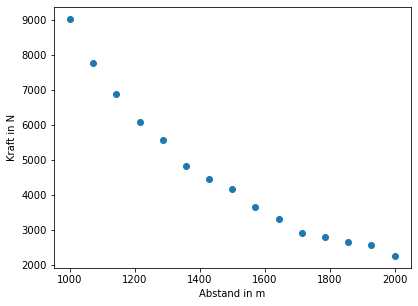
Wir haben jetzt eine wesentlich unglücklichere Situation, aber warum? Weil, wir hier keine klare Form für die Punkte, wie eine gerade Linie, haben. Diese Kurve kann zunächst Teil einer Parabel, eines Kreissegments oder einer Exponentialfunktion sein.
Versuchen wir, mit physikalischer Intuition einige Möglichkeiten auszuschließen.
Es ist vernünftig anzunehmen, dass die Tendenz der Kraftabnahme mit zunehmender Entfernung gleich bleiben sollte. Daher werden wir nur nach Funktionen suchen, die monoton abnehmen, d. h. Funktionen, die mit zunehmendem Abstand immer kleiner werden. Dies allein schließt die Parabel und den Kreis aus, weil diese Funktionen irgendwann anfangen würden, sich zu vergrößern. Das bedeutet auch, dass keine positiven geraden Potenzen des Abstandes berücksichtigt werden müssen.
