Wir kümmern uns am Anfang des Jahres mit Ladungen, die sich innerhalb von homogene elektromagnetische Felder bewegen. Dafür brauchen wir kurz eine Wiederholung von Kinematik.
In der Kinematik haben wir in der Vergangenheit hauptsächlich 3 Arten von Bewegungen untersucht:
• Gleichförmige Bewegung
\(a(t)=0\)
\(v(t)=v_0\)
\(s(t)=s_0+v_0\cdot t\)
• Beschleunigte Bewegung
\(a(t)=a_0\)
\(v(t)=v_0+a_0\cdot t\)
\(s(t)=s_0+v_0\cdot t +\frac{1}{2}\cdot a\cdot t^2\)
• Kreisbewegung
\(F_{ZP}=\frac{mv^2}{r}\)
Das ist natürlich nicht alles, was man über diese Themen wissen muss, aber es sind die wichtigsten Ideen, um die elektrischen Phänomene des Semesters zu interpretieren. An diesem Punkt des Kurses werden wir versuchen, das, was wir über elektrische Felder gelernt haben, mit dem zu verbinden, was wir über die Beschreibung von Bewegung gelernt haben.
Das Ziel hier ist die Untersuchung geladener Teilchen, die sich mit konstanter Geschwindigkeit in homogene elektromagnetischen Feldern bewegen. Dazu werden wir zunächst die elektrischen Felder und dann die magnetischen Felder betrachten.
Im Wesentlichen gibt es zwei Beziehungen zwischen dem E-Feld und dem Teilchen, die wir beschreiben können: Die Geschwindigkeit parallel zum Feld und die Geschwindigkeit senkrecht zum Feld. Natürlich können wir beides miteinander mischen und eine Geschwindigkeit erhalten, die einen beliebigen Winkel mit dem Feld bildet, aber das spielt jetzt keine Rolle, weil die Geschwindigkeit immer in parallele und senkrechte Komponenten zerlegt werden kann.
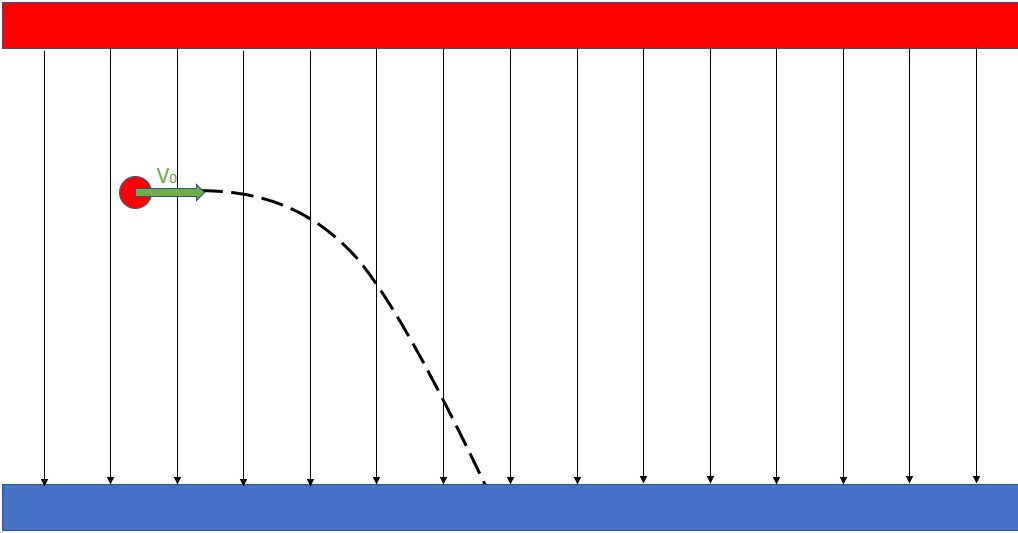
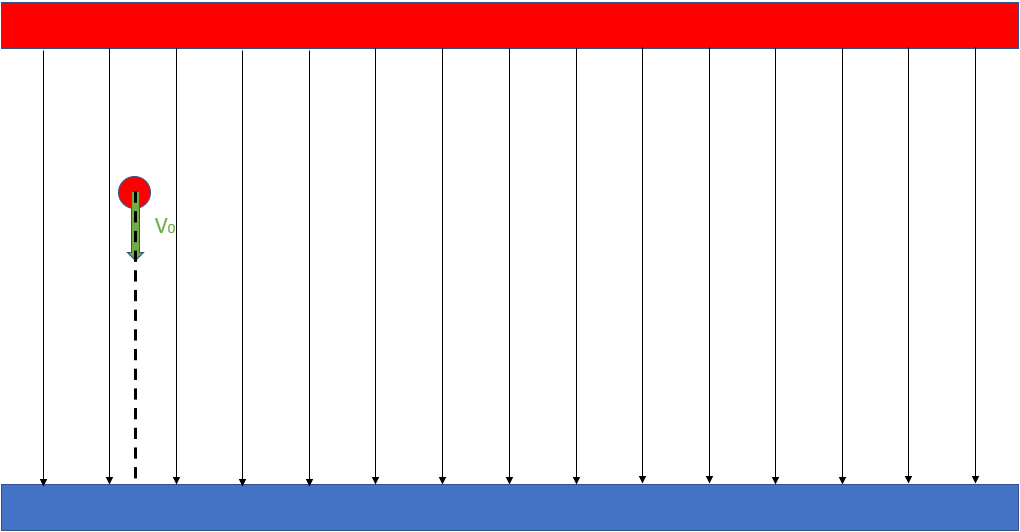
Das Bild kann sehr stark an den schrägen Wurf erinnern, den wir vorher untersucht haben, und es müssten eigentlich noch mehr Ähnlichkeiten auftreten.
Die Situation ist sehr ähnlich bei magnetischen Feldern, bei denen die Anfangsgeschwindigkeit parallel oder senkrecht sein kann und alle Geschwindigkeiten, die nicht ausschließlich zu eine dieser Kategorien gehöhren, zerlegt werden können.
